This chapter[1] first details the formal relationships and distinctions between purely a fortiori argument, a crescendo argument (which refers to proportional a fortiori argument), pro rata argument, and qualitative and quantitative analogy. These various forms of argument are often confused, so it is well to clearly describe and explain them. These general findings are then used to formally analyze the debate between R. Tarfon and the Sages in Mishna Baba Qama 2:5, in the course of which the important dayo (sufficiency) principle is introduced. Thereafter, the Gemara’s take on this Mishnaic passage (in the Babylonian Talmud, Baba Qama 25a-b) is looked at.
1.Formalization of a fortiori argument
Based on close analysis of a large number of Biblical and Talmudic examples (some known to Jewish tradition and some newly identified by me), as well as examples from everyday discourse, I discovered and proposed in my 1995 book Judaic Logic: A Formal Analysis of Biblical, Talmudic and Rabbinic Logic, a detailed description and explanation of (purely) a fortiori argument. In my later, 2013, book, A Fortiori Logic: Innovations, History and Assessments (hereinafter, A Fortiori Logic), I considerably deepened and broadened the analysis of such argument – validating it more precisely and including ‘proportional’ variants of it (a crescendo argument), among other things.
The expression ‘a fortiori (ratione)’ is of Latin origin, meaning ‘with stronger (reason)’. Although we often speak of ‘the a fortiori argument’ as if there is only one form of it, such reasoning has in fact many forms, which however are easily seen to comprise one family. In the present paper, we will only draw attention to some of these forms, labeled ‘copulative’ because the items they concern are terms (rather than theses).
An a fortiori argument consists of three propositions called the major premise, the minor premise and the conclusion. Such an argument comprises four items, which are here always symbolized in the same way. The four items are called the major, the minor, the middle and the subsidiary; and the chosen symbols for them are respectively P, Q, R and S[2].
The four valid moods of concern to us here (those copulative in form) are the following.
- The positive subjectal {+s} mood:
|
P is more R than (or as much R as) Q (is R), |
|
and Q is R enough to be S; |
|
therefore, all the more (or equally), P is R enough to be S. |
Notice that the valid inference goes ‘from minor to major’; that is, from the minor term (Q) to the major one (P); meaning: from the minor term as subject of ‘R enough to be S’ in the minor premise, to the major term as subject of same in the conclusion. Any attempt to go from major to minor in the same way (i.e. positively) would be invalid inference.
- The negative subjectal {–s} mood:
|
P is more R than (or as much R as) Q (is R), |
|
yet P is R not enough to be S; |
|
therefore, all the more (or equally), Q is R not enough to be S. |
Notice that the valid inference goes ‘from major to minor’; that is, from the major term (P) to the minor one (Q); meaning: from the major term as subject of ‘R not enough to be S’ in the minor premise, to the minor term as subject of same in the conclusion. Any attempt to go from minor to major in the same way (i.e. negatively) would be invalid inference.
For examples: granted that Jack (P) can run faster (R) than Jill (Q), it follows that: if Jill can run fast enough to cover one mile in under 15 minutes (S), then surely so can Jack; and if he can’t, then neither can she. Needless to say, the conditions are presumed identical in both cases; we are talking of the same course, in the same weather, in good health, and so on. If different conditions are intended, the argument may not function correctly; in such case, an objection to it can logically be raised.
- The positive predicatal {+p} mood:
|
More (or as much) R is required to be P than (as) to be Q, |
|
and S is R enough to be P; |
|
therefore, all the more (or equally), S is R enough to be Q. |
Notice that the valid inference goes ‘from major to minor’; that is, from the major term (P) to the minor one (Q); meaning: from the major term as predicate of ‘S is R enough to be’ in the minor premise, to the minor term as predicate of same in the conclusion. Any attempt to go from minor to major in the same way (i.e. positively) would be invalid inference.
- The negative predicatal {–p} mood:
|
More (or as much) R is required to be P than (as) to be Q, |
|
yet S is R not enough to be Q; |
|
therefore, all the more (or equally), S is R not enough to be P. |
Notice that the valid inference goes ‘from minor to major’; that is, from the minor term (Q) to the major one (P); meaning: from the minor term as predicate of ‘S is R not enough to be’ in the minor premise, to the major term as predicate of same in the conclusion. Any attempt to go from major to minor in the same way (i.e. negatively) would be invalid inference.
For examples: granted that it takes more strength (R) to lift 50 kilos (P) than 30 (Q): if someone (S) is strong enough to lift 50 kilos, then surely he can lift 30; and if he can’t lift 30, then he can’t lift 50. Needless to say, the conditions are presumed identical in both cases; we are talking of the same handle, on the same day, in good health, and so on. If different conditions are intended, the argument may not function correctly; in such case, an objection to it can logically be raised.
Note that in all four of the above moods, the a fortiori argument is stated categorically only if there are no underlying conditions. Obviously, if there are conditions they ought to be specified, or at least we must ensure they are the same throughout the argument.
Thus, to summarize, there are four valid moods of copulative a fortiori argument: two subjectal moods, in which the major and minor terms (P and Q) are the logical subjects of the three propositions concerned, while the subsidiary term (S) is a predicate; and two predicatal moods, in which the major and minor terms (P and Q) are the logical predicates of the three propositions concerned, while the subsidiary term (S) is a subject. Note well that these two sets of forms, the subjectal and the predicatal, are not interchangeable.
The middle term (R), however, is a predicate in both premises and in the conclusion of all the moods, note well. In subjectal moods it is a predicate of the major and minor terms (P and Q); in the predicatal moods it is a predicate of unspecified subjects in the major premise and a predicate of the subsidiary term (S) in the minor premise and conclusion, the subsidiary term being one instance of the unspecified subject-matter of the major premise.
The major premise is always positive, though it differs in form in subjectal and predicatal arguments. In each of these types, there are two variants: in one, the minor premise and conclusion are positive; and in the other, they are negative. The positive and negative versions in each case are obviously closely related – the minor premise of the one is the negation of the conclusion of the other, and vice versa; that is, each can be used as a reductio ad absurdum for the other.
The difference between subjectal and predicatal moods is called a difference of structure. The difference between positive and negative moods is called a difference of polarity. The difference between moods that go “from minor to major” (i.e. from the minor term in the minor premise to the major term in the conclusion) and those that go “from major to minor” (i.e. from the major term in the minor premise to the minor term in the conclusion) is called a difference of orientation.
Sometimes this difference of direction is stated in Latin, as “a minori ad majus” and “a majori ad minus”. In Hebrew, it is stated as “mi-qal le-chomer” and “mi-chomer le-qal”[3]. Note that the “from” term may be the minor or major and occurs in the minor premise; and the “to” term is accordingly the major or minor, respectively, and occurs in the conclusion. Notice the variations in orientation in accord with the structure and polarity involved.
In sum, these four valid moods are effectively four distinct figures (and not merely moods) of a fortiori argument, since the placement of their terms differs significantly in each case. This is clearly seen in the following table:
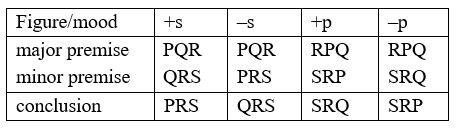
If we look at usage statistics, we find this assertion clearly confirmed[4]. Thus, in the Tanakh (the Jewish Bible), of the 46 a fortiori arguments found, 14 are +s, 13 are –s, 15 are +p and 4 are –p. Again, in the Mishna (the basis of Talmudic law), of the 46 cases found, 32 are +s, 12 are –s, 1 is +p and 1 is –p. Of the 15 cases found in Plato’s works, 9 are +s, 1 is –s, none is +p and 5 are –p. Of the 80 cases found in Aristotle’s works, 50 are +s, 22 are –s, 5 are +p and 3 are –p.
2.Validation of a fortiori argument
Validation of an argument means to demonstrate its validity. An argument is ‘valid’ if, given its premises, its conclusion logically follows. Otherwise, if the putative conclusion does not follow from the given premises, and more so if its denial follows from them, the argument is ‘invalid’. If the putative conclusion is merely not implied by the given premises, it is called a non sequitur (Latin for ‘it does not follow’); in such case, the contradictory of the putative conclusion is logically as compatible with the given premises as the putative conclusion is. If a contrary or the contradictory of the putative conclusion is positively implied by the given premises, the putative conclusion is called an absurdity (lit. ‘unsound’) or more precisely an antinomy (adj. antinomic, lit. ‘against the laws’ of thought).
The validity of an argument does not guarantee that its conclusion is true, note well. An argument may be valid even if its premises and conclusion are in fact false. Likewise, the invalidity of an argument does not guarantee that its conclusion is false. An argument may be invalid even if its premises and conclusion are in fact (separately) true. The validity (or invalidity) of an argument refers to the logical process, i.e. to the claim that a set of premises of this kind formally implies (or does not imply) a conclusion of that kind.
A material a fortiori argument may be validated simply by showing that it can be credibly cast into any one of the valid moods listed above. If it cannot be fitted into one of these (or any other) valid moods, it is invalid – or at least, it is not an a fortiori argument. The validations of the forms of a fortiori argument may be carried out as we will now expound. Invalid forms are forms that cannot be similarly validated. Obviously, material arguments can also be so validated; but the quick way is, as just stated, to credibly cast them into one of the valid forms. Once the forms are validated by logical science, the material cases that fit into them are universally and forever thereafter also validated.
One way to prove the validity of a new form of deduction is through the intermediary of another, better known, form of deduction. Such derivation is called ‘reduction’. ‘Direct’ reduction is achieved by means of conversions or similar immediate inferences. If the premises of the tested argument imply those of an argument already accepted as valid, and the conclusion of the latter implies that of the former, then the tested argument is shown to be equally valid. ‘Indirect’ reduction, also known as reduction ad absurdum, on the other hand, proceeds by demonstrating that denial of the tested conclusion is inconsistent with some already validated process of reasoning.
The validation procedures for a fortiori argument are based on analysis of the meanings of the propositions involved in such argument, i.e. on reduction of these more complex forms to simpler forms more studied and better understood by logicians. This work can be presented briefly as follows:
- Positive subjectal a fortiori argument validation:
The major premise, “P is more R than (or as much R as) Q is,” means:
|
P is R, i.e. P is to a certain measure or degree R (say, Rp); |
|
Q is R, i.e. Q is to a certain measure or degree R (say, Rq); |
|
and Rp is greater than (or equal to) Rq (whence: Rp implies Rq[5]). |
The minor premise, “Q is R enough to be S,” means:
|
Q is to a certain measure or degree R (Rq); |
|
whatever is at least to a certain measure or degree R (say, Rs) is S and |
|
whatever is not at least to that measure or degree R (i.e. is not Rs) is not S;[6] |
|
and Rq is greater than or equal to Rs. |
The conclusion “P is R enough to be S,” is composed of four clauses:
|
P is to a certain measure or degree R (say, Rp); |
|
whatever is at least to a certain measure or degree R (say, Rs), is S; |
|
whatever is not at least to that measure or degree R (i.e. is not Rs), is not S; |
|
and Rp is greater than (or equal to) Rs. |
The four components of this conclusion are obtained as follows: the first from the major premise, the second and third from the minor premise, and the fourth from the tabulated quantitative argument (see below) which is drawn from both premises. Here, note well, the “enough R” condition of the conclusion (implied in its second and third components) comes from the minor premise, because it concerns the subsidiary term (S). Here, then, the crucial threshold value of R is Rs, i.e. the minimum value of R needed to be S; knowing that Rq equals or exceeds Rs, we can predict that Rp does so too.
- Positive predicatal a fortiori argument validation:
The major premise, “More (or as much) R is required to be P than to be Q,” means:
|
Only what is at least to a certain measure or degree R (say, Rp) is P; |
|
only what is at least to a certain measure or degree R (say, Rq) is Q; |
|
and Rp is greater than (or equal to) Rq (whence: Rp implies Rq[7]). |
The minor premise, “S is R enough to be P,” means:
|
S is to a certain measure or degree R (say, Rs); |
|
whatever is at least to a certain measure or degree R (Rp) is P, and |
|
whatever is not at least to that measure or degree R (i.e. is not Rp) is not P;[8] |
|
and Rs is greater than or equal to Rp. |
The conclusion “S is R enough to be Q,” is composed of four clauses:
|
S is to a certain measure or degree R (say, Rs); |
|
whatever is at least to a certain measure or degree R (say, Rq), is Q; |
|
whatever is not at least to that measure or degree R (i.e. is not Rq), is not Q; |
|
and Rs is greater than (or equal to) Rq. |
The four components of this conclusion are obtained as follows: the first from the minor premise, the second and third from the major premise, and the fourth from the tabulated quantitative argument (see below) which is drawn from both premises. Here, note well, the “enough R” condition of the conclusion (implied in its second and third components) comes from the major premise, because it concerns the minor term (Q). Here, then, the crucial threshold value of R is Rq, i.e. the minimum value of R needed to be Q; knowing that Rp equals or exceeds Rq, we can predict that Rs does so too.
Note that in both the above moods, the conclusion of the a fortiori argument comes solely and entirely from the two premises together (not separately). It is true that the premises contain more information than the conclusion does; but that only means that not all the information in them is used. This does not signify redundancies in the premises, because their form is essential to intuitive human understanding of the argument, whose conclusion has similar form to the minor premise.
As regards, the corresponding negative moods, they are most easily validated by reductio ad absurdum. There is no pressing need to interpret their negative propositions. We say: suppose the putative conclusion is denied, then combining such denial with the same major premise we would obtain a denial of the given minor premise; this being absurd, the putative conclusion must be valid.
It is important to grasp the intent of the word “enough” (or “sufficiently”) in the minor premises and conclusions above detailed. These tell us that the subject has whatever amount of R it takes to merit the predicate; i.e. that the subject has at least the amount of R required for the predicate. The word “enough” informs us that there is a threshold value of R as of and above which the subject indeed has the predicate, but anywhere before which the subject does not have the predicate; the R-value of the subject is then specified as falling on the required side of the known threshold.
Note also that ‘The subject is R enough to have the predicate’ implies ‘The subject has the predicate’ provided R is indeed by itself enough for the predication. If R is in fact only part of a set of conditions necessary for the predicate, then factor R cannot be truthfully said to be ‘enough’ for the predication – or, if it happens to be proposed as ‘enough’ for the predication, the remaining required factors must at least be tacitly intended.[9]
It is also important to notice the utility of the threshold condition, i.e. the implication of the minor premise that there is a threshold value of R which has to be reached or surpassed before the subject can accede to a certain predicate, i.e. that not all values of R fit the bill. If all values of R were sufficient for the predication, then we could easily deduce the desired conclusion by mere syllogism.
In the case of positive subjectal argument, we would say: given (hypothetically) that all R are S, then since P is R (implied by the major premise), it follows (even without recourse to the ‘Q is S’ implied by the minor premise) that P is S (desired conclusion). In the case of positive predicatal argument, we would say: given (hypothetically) that all R are Q, then since all P are R (implied by the major premise requirement) and S is P (implied by the minor premise), it follows that S is R and thence that S is Q (desired conclusion).
Clearly, in both these eventualities the argument would be merely syllogistic, and not at all function like an a fortiori argument. Thus, the threshold condition is essential to the formation of a genuine a fortiori argument; it is not something that can be ignored or discarded. Many people think that a fortiori argument can be formulated without this crucial condition, but that is a grave error on their part.
What transpires in the above analysis is that the middle term (R) of copulative argument is its essential element. Because the middle term R underlies the three other terms (the major term P, the minor term Q, and the subsidiary term S), we can say that a fortiori argument is principally about it, and only incidentally about them. The middle term is the core or center of gravity of the whole argument; it is the common ground and intermediary of the three other terms.
What a fortiori argument does is to relate together three values of the middle term R (here symbolized by Rp, Rq and Rs) found in relation to the other three terms and thus representing them. The middle term of a fortiori argument is always something that varies quantitatively, in measure or degree – and the argument constitutes a comparison and hierarchical ordering of its different values (which are given in relation to the three other terms). The truth of all this can be easily seen with reference to the following diagram, where quantities of R on the right are greater than quantities of R on the left.
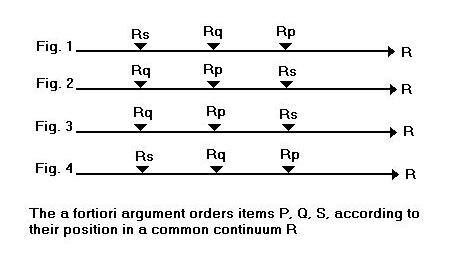
That, then, is the essence of a fortiori argument: it is a comparison between the various quantities (measures or degrees) of the middle term that are copulatively involved in the other three terms (as subjects or predicates, as the case may be). We can thus present the quantitative core of the validations very simply as follows, with reference to the comparative propositions implied in the premises and conclusions. Here, as always, ≥ means ‘is greater than or equal to’ and < means ‘is less than’:
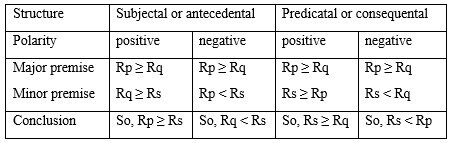
Note that the egalitarian positive subjectal (or antecedental) conclusion Rp = Rs can only be drawn from the premises Rp = Rq and Rq = Rs. Likewise, the egalitarian positive predicatal (or consequental) conclusion Rs = Rq can only be drawn from the premises Rs = Rp and Rp = Rq. In all other positive arguments, the conclusions would be Rp > Rs or Rs > Rq (as the case may be), even if one of the premises concerned involves an equation. It follows that the egalitarian negative argument of subjectal form has premises Rp ≥ Rq and Rp ≠ Rs and conclusion Rq ≠ Rs; while that of predicatal form has premises Rp ≥ Rq and Rs ≠ Rq and conclusion Rs ≠ Rp.
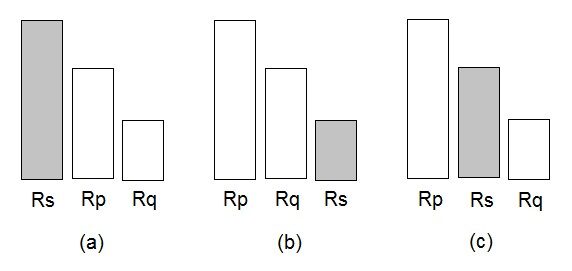
Another way to illustrate the quantitative aspect of a fortiori argument is by means of bar charts, as in the diagram below. Given that Rp is greater than (or equal to) Rq, there are three possible positions for Rs: in (a) Rs is greater than (or equal to) Rp and therefore than (or to) Rq; in (b) Rs is smaller than (or equal to) Rq and therefore than (or to) Rp; and in (c) Rs is in between Rp and Rq, in which case no conclusion can be drawn. Chart (a) can be used to illustrate the positive predicatal and negative subjectal moods, and chart (b) the positive subjectal and negative predicatal moods, while chart (c) can be used to explain invalid arguments.
We have thus formally and indubitably demonstrated all the said moods of a fortiori argument to be valid. As regards invalid a fortiori arguments, the following can be said. If the major item P is not identical in the major premise and in the minor premise or conclusion (so that there are effectively two major items), and/or if the minor item Q is not identical in the major premise and in the minor premise or conclusion (so that there are effectively two minor items), and/or if the middle item R is not identical in the major premise, the minor premise and the conclusion (so that there are effectively two or three middle items), and/or if the subsidiary item S is not identical in the minor premise and the conclusion (so that there are effectively two subsidiary items) – in any such cases, there is illicit process. Needless to say, “identical” here refers to identity not only in the words used, but also in their intentions; we are sometimes able to formulate two terms in such a way as to make them seem the same superficially, although in fact they are not the same deeper down.
Likewise, if an item or a proposition is negative where it should be positive or vice versa – here again, we have fallacious reasoning. Although all such deviations from the established norms are obviously invalid, since we cannot formally validate them, they are often tried by people in practice, so it is worth keeping them in mind.
Qualitative analogy. Many people confuse purely a fortiori argument with qualitative analogy. It is important to clearly see the differences between these argument forms. Analogy may be qualitative or quantitative. Qualitative analogical argument, like pure a fortiori argument, consists of four terms, which we may label P, Q, R, S, and refer to as the major, minor, middle and subsidiary terms as before, although here without implying that the major term is greater in any way than the minor. The argument may then take one of the following four (copulative) forms:
a. The positive subjectal mood. Given that subject P is similar to subject Q with respect to predicate R, and that Q is S, it follows that P is S. We may analyze this argument step by step as follows:
Major premise: P and Q are alike in that both of them have R.
This implies both ‘P is R’ and ‘Q is R’, and is implied by them together.
Minor premise: Q is S.
The term S may of course be any predicate; although in legalistic reasoning, it is usually a legal predicate, like ‘imperative’, ‘forbidden’, ‘permitted’, or ‘exempted’.
Intermediate conclusion and further premise: All R are S.
This proposition is obtained from the preceding two as follows. Given that Q is S and Q is R, it follows by a substitutive third figure syllogism that there is an R which is S, i.e. that ‘some R are S’. This particular conclusion is then generalized to ‘All R are S’, provided of course we have no counter-evidence. If we can, from whatever source, adduce evidence that some R (other than Q) are not S, then of course we cannot logically claim that all R are S. Thus, this stage of the argument by analogy is partly deductive and partly inductive.
Final conclusion: P is S.
This conclusion is derived syllogistically from All R are S and P is R.
If the middle term R is known and specified, the analogy between P and Q will be characterized as ‘complex’; if R is unknown, or vaguely known but unspecified, the analogy between P and Q will be characterized as ‘simple’. In complex analogy, the middle term R is clearly present; but in simple analogy, it is tacit. In complex analogy, the similarity between P and Q is indirectly established, being manifestly due to their having some known feature R in common; whereas in simple analogy, the similarity between them is effectively directly intuited, and R is merely some indefinite thing assumed to underlie it, so that in the absence of additional information we are content define it as ‘whatever it is that P and Q have in common’.
Needless to say, the above argument would be equally valid going from P to Q. I have here presented it as going from Q to P to facilitate comparison and contrast to a fortiori argument. Note in passing that we could similarly validate an argument with a negative major premise. Given that ‘P is dissimilar to Q with respect to R’ (i.e. say, P is R but Q is not R), then since ‘Q is S’, there is an S which is not R, whence by generalization No S is R, and this together with P is R implies that ‘P is not S’.
Positive subjectal qualitative analogical argument has, then, in brief the following form: Given that P and Q are alike in having R, and that Q is S, it follows that P is S. The validation of this argument is given in our above analysis of it. What we see there is that the argument as a whole is not entirely deductive, but partly inductive, since the general proposition ‘All R are S’ that it depends on is obtained by generalization.
Thus, it may well happen that, given the same major premise, we find (empirically or through some other reasoning process) that Q is S but P is not S. This just tells us that the generalization to ‘All R are S’ was in this case not appropriate – it does not put analogical argument as such in doubt. Such cases might be characterized as ‘denials of analogy’ or ‘disanalogies’. Note also that if ‘All R are S’ is already given, so that the said generalization is not needed, then the argument as a whole is not analogical, but entirely syllogistic; i.e. it is: All R are S and P is R, therefore P is S. Thus, analogy as such is inherently inductive. And obviously, simple analogy is more inductive than complex analogy, since less is clearly known and sure in the former than in the latter.
The above, prototypical mood was positive subjectal. Let us now consider the other possible forms of analogical argument.
b. The negative subjectal mood. Given that subject P is similar to subject Q with respect to predicate R, and that P is not S, it follows that Q is not S.
This mood follows from the positive mood by reductio ad absurdum: given the major premise, if Q were S, then P would be S; but P is not S is a given; therefore, Q is not S. This argument is of course just as inductive as the one it is derived from; it is not deductive.
c. The positive predicatal mood. Given that predicate P is similar to predicate Q in relation to subject R, and that S is P, it follows that S is Q. We may analyze this argument step by step as follows:
Major premise: P and Q are alike in that R has both of them.
This implies both ‘R is P’ and ‘R is Q’, and is implied by them together.
Minor premise: S is P.
Intermediate conclusion and further premise: S is R.
This proposition is obtained from the preceding two as follows. Given that R is P, it follows by conversion that there is a P which is R, i.e. that ‘some P are R’, which is then generalized to ‘all P are R’, provided of course we have no counter-evidence. If we can, from whatever source, adduce evidence that some P are not R, then of course we cannot logically claim that all P are R. Next, using this generality, i.e. ‘all P are R’, coupled with the minor premise ‘S is P’, we infer through first figure syllogism that ‘S is R’. Clearly, here again, this stage of the argument by analogy is partly deductive and partly inductive.
Final conclusion: S is Q.
This conclusion is derived syllogistically from R is Q and S is R.
Note that the generalized proposition here concerns the major and middle terms, whereas in the preceding case it concerned the middle and subsidiary terms. Needless to say, this argument would be equally valid going from Q to P. I have here presented it as going from P to Q to facilitate comparison and contrast to a fortiori argument.
d. The negative predicatal mood. Given that predicate P is similar to predicate Q in relation to subject R, and that S is not Q, it follows that S is not P.
This mood follows from the positive mood by reductio ad absurdum: given the major premise, if S were P, then S would be Q; but S is not Q is a given; therefore, S is not P. This argument is of course just as inductive as the one it is derived from; it is not deductive.
It is clear from the above presentation why purely a fortiori argument and qualitative analogical argument cannot be equated, even though they superficially might seem the same. The former is unidirectional (except in egalitarian cases) and deductive, whereas the latter is bidirectional and more inductive. Moreover, neither should be confused with syllogistic argument, though some such inference is involved in both.
3.Arguments involving proportionality
A fortiori argument as above described and explained refers more specifically to purely a fortiori argument. In such argument, notice, the subsidiary term S is exactly the same in the minor premise and in the conclusion. However, it is important to realize that there is another class of a fortiori argument, which we shall refer to as a crescendo argument, in which the subsidiary term S is greater or lesser in the minor premise and in the conclusion. Both types are a fortiori argument, and both are often used in practice; but whereas the former type is ‘non-proportional’, the latter type is ‘proportional’.
A crescendo argument. In purely a fortiori argument, there are only four terms, namely P, Q, R and S; whereas, in a crescendo argument, there are effectively five terms, namely P, Q, R and S1 and S2, where S1 and S2 signify two different degrees or measures of S, somewhat ‘proportional’ to P and Q (or Q and P, as the case may be) – or more precisely, as we shall see, to Rp and Rq (or Rq and Rp, as the case may be). A crescendo argument also differs from purely a fortiori argument in that it contains (tacitly, if not explicitly) an additional premise about proportionality. That is, whereas the ‘non-proportional’ forms of the argument have only two premises (the major and the minor), the ‘proportional’ forms have a third premise (which specifies the proportionality involved).
The following are the four forms of a crescendo argument corresponding to the earlier listed forms of purely a fortiori argument (leaving out egalitarian possibilities, for simplicity):
The positive subjectal, which goes from minor to major:|
P is more R than Q (is R) [i.e. Rp > Rq] |
|
and Q is R enough [i.e. it is Rq] to be S [i.e. it is Sq], |
|
and S varies in proportion to R [additional premise of proportionality]; |
|
therefore, P is R enough [i.e. it is Rp] to be more than S [i.e. it is Sp, which is > Sq]. |
The negative subjectal, which goes from major to minor:
|
P is more R than Q (is R) [i.e. Rp > Rq] |
|
and P is not R enough [i.e. it is not Rp] to be S [i.e. it is not Sp], |
|
and S varies in proportion to R [additional premise of proportionality]; |
|
therefore, Q is not R enough [i.e. it is not Rq] to be less than S [i.e. it is not even Sq, which is < Sp]. |
The positive predicatal, which goes from major to minor:
|
More R is required to be P than to be Q [i.e. Rp > Rq], |
|
and S [i.e. Sp] is R enough [i.e. it is Rp] to be P, |
|
and R varies in proportion to S [additional premise of proportionality]; |
|
therefore, less than S [i.e. Sq, which is < Sp] is R enough [i.e. it is Rq] to be Q. |
The negative predicatal, which goes from minor to major:
|
More R is required to be P than to be Q [i.e. Rp > Rq], |
|
and S [i.e. Sq] is not R enough [i.e. it is not Rq] to be Q, |
|
and R varies in proportion to S [additional premise of proportionality]; |
|
therefore, more than S [i.e. Sp, which is > Sq] is not R enough [i.e. it is not Rp] to be P. |
Note the difference in orientation of the additional premise in subjectal and predicatal arguments (in the former S is proportional to R, whereas in the latter R is proportional to S). Note well that these premises about proportionality are needed for the respective arguments to be valid; if such additional premise is not applicable in a given case, the a crescendo argument is not valid, even if the purely a fortiori argument is valid. In other words, not all a fortiori arguments are a crescendo arguments – some are purely a fortiori. Many people (for instance, the writer of the Gemara Baba Qama 25a) fail to understand this, and think that proportionality is universally applicable. Conversely, many people (for instance, Hyam Maccoby[10]) think that only purely a fortiori argument is valid.
Pro rata argument. Argument a crescendo (i.e. ‘proportional’ a fortiori) should not be confused with argument by proportion, which we can refer to as argument pro rata (this Latin name being already well established in the English language), this being understood to mean “at the same rate.” Such argument concerns concomitant variations between two variables, and may be formulated as follows:
|
Y varies in proportion to X. Therefore: |
|
given that: if X = x, then Y = y, |
|
it follows that: if X = more (or less) than x, then Y = more (or less) than y. |
An example of it is Aristotle’s statement: “Every good quality of the soul, the higher it is in degree, so much more useful it is” (Politics 7:1), which intends the argument: given that a certain quality of the soul is good, it is useful; if it is improved, it is still more useful. In practice, pro rata argument is often expressed in the form: “the more X, the more Y; and (by implication) the less X, the less Y.” Note that two variants (which mutually imply each other) are possible: one with “more” and one with “less” – that is, the argument can go either way, increasing or decreasing the quantities involved.
The statement “Y varies in proportion to X” is not an argument but a mere proposition, reflecting some generalized empirical observations or a more theoretical finding. The pro rata argument includes this proposition as its major premise, but requires an additional minor premise (viz. “if X = x, then Y = y”) to draw the conclusion (“if X = more/less than x, then Y = more/less than y”). The conclusion mirrors the minor premise in form, but its content is intentionally different. The quantities involved do not stay the same, but increase or decrease (as the case may be).
Notice that a pro rata argument has no middle term, unlike an a fortiori one. A pro rata argument is thus more akin to apodosis than to syllogism. Its major premise sets a broad principle, of which the minor premise and conclusion are two applications. The argument involved is thus simply inference of one quantity from another within the stated principle. If we found that contrary to expectations X and Y do not vary concomitantly as above implied, we would simply deny the major premise. In other words, this argument is essentially positive in form. A negative mood of it (with the same major premise and denials of the previous conclusion and minor premise) would not make much sense, since its minor premise and conclusion would be in conflict with its major premise.
The above formulas are at least true in cases of direct proportionality; in cases of inverse proportionality, the language would be: “the more X, the less Y; and (by implication) the less X, the more Y;” and the argument would have the following form:
|
Y varies in inverse proportion to X. Therefore: |
|
given that: if X = x, then Y = y, |
|
it follows that: if X = more (or less) than x, then Y = less (or more) than y. |
And of course, in more scientific contexts, we may have access to a more or less complex mathematical formula – say Y = f(X), where f refers to some function – an equation that allows precise calculation of the proportion involved. In other words, the validity of pro rata argument is not always obvious and straightforward, but depends on our having a clear and reliable knowledge of the concomitant variation of the values of the terms X and Y. Given such knowledge, we can logically justify drawing the said conclusions from the said premises. Lacking it, we are in a quandary.
As its name implies, pro rata argument signifies that there is (if only approximately) some constant rate in the relative fluctuations in value of the variables concerned. The variables X and Y may be said to be proportional if X/Y = a constant, or inversely proportional if XY = a constant. In the exact sciences, of course, such a constant is a precisely measurable quantity; but in everyday pro rata discourse, the underlying ‘constant’ is usually a vague quantity, perhaps a rough range of possible values.
Proportionality or inverse proportionality as just defined, which can be represented by a straight line graph, and even when the graphical representation is more curved (e.g. exponential), may be characterized as simple. It becomes complex, when there are ups and downs in the relation of the two variables, i.e. when an increase in X may sometimes imply an increase in Y and sometimes a decrease in Y, it is obviously not appropriate to formulate the matter in the way of a standard pro rata argument. In such cases, we would just say: “the values of X and Y can be correlated in accord with such and such a formula,” and then use the formula to calculate inferred quantities.
Proportionality may be continuous or not. Sometimes, there is proportionality of sorts, but it comes in slices: e.g. from X = 0 to 1, Y = k; from X = 1 to 2, Y = k +1; etc. That is, to each range of values for X, there corresponds a certain value of Y, and the two quantities go increasing (or decreasing, as the case may be). Such proportionality is compatible with pro rata argument. For this reason, it is wise to put the word ‘proportionality’ in inverted commas, so as to remember that it does not always imply continuity.
Note too that proportionality may be natural or conventional. An example of the latter would be a price list: bus fares for children under 16, $1; for adults 16+, $2. However, beware in such case of frequent exceptions or reversals: e.g. unemployed and pensioners, $1. In such cases, any pro rata argument must be stated conditionally: the bus fares are ‘proportional’ to age, provided the adults are not unemployed or pensioners.
It should also be reminded that proportionality (or its inverse), simple or complex, may or may not be indicative of a causal relation (in the various senses of that term). Two variables may vary concomitantly by virtue of being effects of common causes, in which case we refer to parallelism between them, or the one may cause or be caused by the other. Also, of course, such parallelism or causality may be unconditional or conditional. In such cases as it is unconditional, no more need be said. But in such cases as it is conditional, the condition(s) should ideally be clearly stated, although often they are not.
Pro rata argument may occur in discourse independently of a fortiori argument, or in conjunction with such argument. In any case, it should not be confused with a fortiori argument: they are clearly different forms of reasoning. Pro rata involves only two terms, or more precisely two values (or more) of two variables; whereas a fortiori involves four distinct terms, which play very different roles in the argument. Pro rata and a fortiori are both analogical arguments of sorts, but the former is much simpler than the latter.
The validation process. A crescendo argument can be viewed as a combination of a fortiori argument and pro rata argument. This could be expressed as a formula:
A crescendo = a fortiori cum pro rata.
That is, we can divide a crescendo argument in two stages. In the case of positive subjectal argument: first, we draw the purely a fortiori conclusion “P is R enough to be Sq (the original value of S),” and then by means of pro rata reasoning we increase the conclusion to “P is R enough to be Sp (the greater value of S).” The pro rata argument used is:
|
If, moreover, (for things that are both R and S,) we find that: S varies in proportion to R, then: |
|
knowing from the above minor premise that: if R = Rq, then S = Sq, |
|
it follows in the conclusion that: if R = more than Rq = Rp, then S = more than Sq = Sp. |
Note that this pro rata stage relies not only on information given in the additional premise, but also on information given in the minor premise[11]. Similarly, in the case of positive predicatal argument, first, we draw the purely a fortiori conclusion “Sp (the original value of S) R enough to be Q” and then by means of pro rata reasoning we decrease the conclusion to “Sq (the lesser value of S) R enough to be Q.” Here, the pro rata argument used is:
|
If, moreover, (for things that are both R and P or Q,) we find that: R varies in proportion to S, then: |
|
knowing from the above minor premise that: if S = Sp, then R = Rp, |
|
it follows in the conclusion that: if S = less than Sp = Sq, then R = less than Rp = Rq. |
Here again the pro rata stage relies not only on information given in the additional premise, but also on information given in the minor premise[12]. All this holds assuming, as earlier specified, that the proportionality proposed in the major premise of the pro rata argument is direct and simple.
These validation procedures for the positive moods show clearly that the validity of a crescendo argument depends on both its a fortiori constituent and its pro rata constituent. A crescendo is neither equivalent to the former nor equivalent to the latter, but emerges from the two together. As for the negative moods, they can as usual be validated by reductio ad absurdum from the positive moods.
What we have done above is to formally demonstrate that, although drawing a ‘proportional’ conclusion from the premises of a valid a fortiori argument is not unconditionally valid, it is also not unconditionally invalid. Such a conclusion is in principle invalid, but it may exceptionally, under specifiable appropriate conditions, be valid. Formally, all depends on whether a pro rata argument can be truthfully proposed in addition to the purely a fortiori argument. In other words, to draw a valid a crescendo conclusion, the premises of a valid a fortiori argument do not suffice; but if they are combined with the fitting premises of a valid pro rata argument, as above detailed, such a conclusion can indeed be formally justified.
Of course, as with all deduction, even if in a given case the inferential process we propose is ideally of valid form, we must also make sure that the premises it involves are indeed true, i.e. that the content of the argument is credibly grounded in fact. Very often, in a crescendo argument, the process is convincing, but the major premise of the implicit pro rata argument is of doubtful truth; this is obviously something to be careful about. Merely declaring a certain proportionality to be true does not make it true – we have to justify all our premises, as well as their logical power to together produce the putative conclusion.
Sometimes, unfortunately, rhetoric comes into play here, and albeit the lack of mathematical proof, the conclusion is made to seem more precise than deductive logic allows. We could at best refer to such conclusions as intuitively reasonable, or as inductive hypotheses, partly but not wholly sustained by the data in the premises; but we must realize and acknowledge that they are not deductive certainties. Otherwise, we would be engaged in misleading sophistry. Thus, it is important to keep in mind that, while we have shown that a crescendo argument is in principle, i.e. under ideal conditions, valid – it does follow that every a crescendo argument put forward in practice, i.e. in everyday or scientific discourse, is valid. It is potentially valid, but not necessarily actually valid. We have to carefully scrutinize each case.
Quantitative analogy. Many people confuse a crescendo argument, which is a special case of a fortiori argument, with quantitative analogy. It is important to clearly see the differences between these argument forms. Analogy may be qualitative or quantitative. The four moods of quantitative analogical argument are as follows:
- The positive subjectal mood: Given that subject P is greater than subject Q with respect to predicate R, and that Q is S (Sq), and that the ratio of Sp to Sq is the same as the ratio of P to Q (with respect to R), it follows that P is proportionately more S (Sp).
Note that the additional premise about the ratios being the same is very often tacit, though sometimes explicit. Moreover, very often in practice the ratios are in fact not exactly the same, but only roughly the same. Also, the reference to the ratio of P to Q (with respect to R) should perhaps be more precisely expressed as the ratio of Rp to Rq. Note that this argument effectively has five terms instead of only four (since term S splits off into two terms, Sp and Sq). Of course, the additional premise about proportionality is usually known by inductive means. It might initially be assumed, and thereafter found to be untrue or open to doubt.
The argument here is, more briefly put: ‘just as P > Q, so Sp > Sq’. We can similarly argue ‘just as P < Q, so Sp < Sq’, or ‘just as P = Q, so Sp = Sq’. In other words, positive subjectal quantitative analogy may as well be from the inferior to the superior (as in the initial case), from the superior to the inferior, or from equal to equal; it is not restrictive with regard to direction. In this respect, it differs radically from positive subjectal a crescendo argument, which only allows for inference from the inferior to the superior, or from equal to equal, and excludes inference from the superior to the inferior. All this seems obvious intuitively; having validated the qualitative analogy, all we have left to validate here is the idea of ratios, and that is a function of mathematics.
As regards negation of the major premise, here, we can deal with it very simply as follows. ‘P is not greater than Q with respect to R’ can be restated as ‘P is either lesser than or equal to Q with respect to R’; therefore, given that Q is Sq and that Sp:Sq = P:Q (or Rp:Rq), it follows that P is Sp, where Sp < or = Sq. In other words, when the major premise is negative, we resort to two positive quantitative analogies in its stead.
- The negative subjectal mood: Given that subject P is greater than subject Q with respect to predicate R, and that P is not S (Sp), and that the ratio of Sp to Sq is the same as the ratio of P to Q (with respect to R), it follows that Q is not proportionately less S (Sq).
This mood can be validated by reductio ad absurdum to the positive one. Both the major premise (viz. that P > Q, with respect to R) and the additional premise about proportionality (viz. that Sp:Sq = Rp:Rq) remain unchanged. What has ‘changed’ is that the minor premise of the negative mood is the denial of the conclusion of the positive mood, and the conclusion of the negative mood is the denial of the minor premise of the positive mood. Note that here instead of ‘not more S (Sp)’ and ‘not S (Sq)’, I have put ‘not S (Sp)’ and ‘not less S (Sq)’; this is done only to preserve the normal order of thought – it does not affect the argument as such. Here again, needless to say, though the mood shown is based on P > Q, it can easily be reformulated with P < Q or P = Q; this only affects the conclusion’s magnitude (making Sq mean ‘more S’ or ‘equally S’ as appropriate).
- The positive predicatal mood: Given that predicate P is greater than predicate Q in relation to subject R, and that a certain amount of S (Sp) is P, and that the ratio of Sp to Sq is the same as the ratio of P to Q (in relation to R), it follows that a proportionately lesser amount of S (Sq) is Q.
Here, the argument is essentially that ‘just as P > Q, so Sp > Sq’, i.e. that the amounts of subject S (viz. Sp and Sq) in the minor premise and conclusion differ in accord with the amounts of predicates P and Q (in relation to R). Or maybe we should say that subject R differs in magnitude or degree when its predicate is P (Rp) and when its predicate is Q (Rq), and that subject S differs accordingly (i.e. Sp and Sq differ in the same ratio as Rp to Rq). This is again an inductive argument; and it would be equally valid in the forms ‘just as P < Q, so Sp < Sq’, or ‘just as P = Q, so Sp = Sq’.
- The negative predicatal mood: Given that predicate P is greater than predicate Q in relation to subject R, and that a certain amount of S (Sq) is not Q, and that the ratio of Sp to Sq is the same as the ratio of P to Q (in relation to R), it follows that a proportionately greater amount of S (Sp) is not P.
This mood can be validated by reductio ad absurdum to the positive one. That is, given the same major premise and additional premise about proportionality, we would say: since the lesser amount of S (Sq) is not Q, it must be that the greater amount of S (Sp) is not P. Here again, if the major premise has P < Q or P = Q instead of P > Q, the conclusion follows suit (i.e. Sp < or = instead of > Sq).
As regards comparison and contrast between quantitative analogy and a crescendo argument, the following need be said. The major premises are the same in both. But the minor premises and conclusions obviously differ, insofar as in quantitative analogy there is no idea of a threshold value of the middle term as there is in a fortiori argument. This explains why the ‘proportionality’ is bidirectional in quantitative analogical argument (inference is always possible both from minor to major and from major to minor); whereas it is clearly unidirectional in a fortiori argument (inference is only possible from minor to major in positive subjectal and negative predicatal argument, and from major to minor in negative subjectal and positive predicatal argument).
Clearly, while qualitative analogy is somewhat comparable to purely a fortiori argument, and quantitative analogy is somewhat comparable to a crescendo argument, these pairs of arguments are still far from logically the same. As can be shown by detailed formal analysis, neither argument can be reduced to the other. However, every valid a fortiori argument incidentally implies a corresponding argument by analogy involving less information and certainty (even if, of course, there is in practice no point in resorting to such implication, given an a fortiori argument, since it is better in all respects).
4.A few words on the history
There are 5 instances of qal vachomer (a fortiori) argument in the Torah (the five books of Moses); and at least another 41 instances in the Nakh (the rest of the Jewish Bible). There 46 instances of the argument in the Mishna, and hundreds more appear in the Gemara and other literature of Talmudic times. (The Mishna is the prime treatise of Judaic jurisprudence, compiled c. 200 CE after some 200 years of discussion of Torah law; this in turn forms the basis of the two Talmuds. The Gemara is essentially a collection of commentaries on the Mishna, given in the Jerusalem Talmud, compiled in c. 400 CE, and in the Babylonian Talmud, compiled in c. 600 CE.)
Clearly, Judaism has from its inception resorted to a fortiori argument (and indeed, in its many varieties). Although the argument is pretty universal, being also found in Greek and Roman discourse, and later in Christian and Islamic discourse, and even in faraway Indian and Chinese discourse, it is evident that its presence in Jewish discourse is independent.
One proof of this is that the early rabbis, never made an effort to formally analyze the argument, only using it intuitively; whereas Greek and Roman sources, including Aristotle[13] and Cicero[14], tried to expose and discuss the argument in relatively general terms. If the rabbis had studied these authors’ works, they would surely have said more about the argument. The rabbis were content to merely name the argument, albeit somewhat descriptively (as having to do with qal-leniency and chomer-stringency), without further ado.
Nevertheless, they mastered this form of reasoning very well in practice (with a few notable exceptions); and they resorted to it very often. There were, to be sure, much later, many attempts by Jewish commentators to clarify and explain a fortiori argument in more formal terms. The most outstanding of these attempts was that of R. Moshe Chaim Luzzatto (the Ramchal, 1707-1746), who listed in his The Book of Logic[15] four moods corresponding to the positive and negative, subjectal and predicatal moods of purely a fortiori argument – without, however, mentioning the threshold condition needed for validation, and therefore without effective validation.
The history of a fortiori argument is a fascinating topic, which I try to deal with in my book A Fortiori Logic is considerable detail, but we cannot say more about it in the present paper. Here, I will be content to very briefly analyze the most important occurrence of a fortiori argument in the Mishna (namely, Baba Qama 2:5), and still more briefly discuss the Gemara take on the latter (in Baba Qama, 25a-b). This Mishna is important due to its introduction of the dayo (sufficiency) principle, which is thereafter often used in Talmudic discourse.
5.Mishna Baba Qama 2:5
The said Mishna reports a debate between the Sages (hachakhamim) and R. Tarfon on the concrete issue of the financial liability of the owner of an ox which causes damages by goring on private property. The Sages consider that the owner must pay for only half the damages, whereas R. Tarfon advocates payment for all the damages. The Sages, though unnamed, were probably important rabbis such as R. Eleazar b. Azariah, R. Ishmael b. Elisha, R. Akiva, and R. Jose haGelili; and R. Tarfon was certainly their equal in status. The Mishna states[16]:
“R. Tarfon there upon said to them: seeing that, while the law was lenient to tooth and foot in the case of public ground allowing total exemption, it was nevertheless strict with them regarding [damage done on] the plaintiff's premises where it imposed payment in full, in the case of horn, where the law was strict regarding [damage done on] public ground imposing at least the payment of half damages, does it not stand to reason that we should make it equally strict with reference to the plaintiff’s premises so as to require compensation in full?
Their answer was: it is quite sufficient that the law in respect of the thing inferred should be equivalent to that from which it is derived: just as for damage done on public ground the compensation [in the case of horn] is half, so also for damage done on the plaintiff's premises the compensation should not be more than half.
R. Tarfon, however, rejoined: but neither do I infer horn [doing damage on the plaintiff's premises] from horn [doing damage on public ground]; I infer horn from foot: seeing that in the case of public ground the law, though lenient with reference to tooth and foot, is nevertheless strict regarding horn, in the case of the plaintiff's premises, where the law is strict with reference to tooth and foot, does it not stand to reason that we should apply the same strictness to horn?
They, however, still argued: it is quite sufficient if the law in respect of the thing inferred is equivalent to that from which it is derived. Just as for damage done on public ground the compensation [in the case of horn] is half, so also for damage done on the plaintiff's premises, the compensation should not be more than half.”
Note that only three amounts of compensation for damages are considered as relevant in the present context: nil, half or full; there are no amounts in between or beyond these three, because the Torah never mentions any such other amounts. No punitive charges are anticipated.
(a) Presented briefly, and in a nested manner, R. Tarfon first argument may be paraphrased as follows:
|
If damage by tooth & foot, then: |
|
if on public grounds, zero compensation, and |
|
if on private grounds, full compensation. |
|
Likewise, if damage by horn, then: |
|
if on public grounds, half compensation, and |
|
if on private grounds, full compensation. |
R. Tarfon’s first putative conclusion is that there should be full payment for damage on private property. The Sages disagree with him, advocating half payment only, saying “dayo—it is enough.”
(b) R. Tarfon then tries another tack, using the same data in a different order. Presented briefly and in a nested manner, this second argument reads as follows:
|
If damage on public grounds, then: |
|
if by tooth & foot, zero compensation, and |
|
if by horn, half compensation. |
|
Likewise, if damage on private grounds, then: |
|
if by tooth & foot, full compensation, and |
|
if by horn, full compensation. |
R. Tarfon’s second putative conclusion is again that there should be full payment for damage on private property. The Sages disagree with him again, advocating half payment only, saying “dayo—it is enough.”
Now, the first thing to notice is that R. Tarfon’s two arguments contain the exact same given premises and aim at the exact same conclusion, so that to present them both might seem like mere rhetoric (either to mislead or out of incomprehension). The two sets of four propositions derived from the above two arguments (by removing the nesting) are obviously identical. All he has done is to switch the positions of the terms in the antecedents and transpose premises. The logical outcome seems bound to be the same. However, as we shall soon realize, the ordering of the terms and propositions does make a significant difference. And we shall see precisely why that is so.
To begin with, let me say that these arguments could well be interpreted as mere arguments by analogy (ratios). In the first case, he is saying just as half is greater than zero, so ‘greater than half’ must mean full. In the second case, he is saying just as half is greater than zero, so ‘greater than full’ must mean full. (Remember, the discussion revolves around only three values: zero, half or full.) But we shall here assume, as traditionally done, that the arguments are a fortiori – it is not unreasonable to do so.
In this perspective, R. Tarfon’s first argument may be depicted as a crescendo, as follows:
|
Private domain damage (P) implies more legal liability (R) than public domain damage (Q) [as we know by extrapolation from the case of tooth & foot]. |
|
For horn, public domain damage (Q) implies legal liability (Rq) enough to make the payment half (Sq). |
|
The payment due (S) is ‘proportional’ to the degree of legal liability (R). |
|
Therefore, for horn, private domain damage (P) implies legal liability (Rp) enough to make the payment full (Sp = more than Sq). |
In that case, the Sage’s first dayo rebuttal seems to intend: no, do not draw a ‘proportional’ conclusion (full compensation), but only infer the same quantity in conclusion (half compensation). That is, the Sages seem to be rejecting the additional premise about proportionality, and limiting the argument to its purely a fortiori dimension:
|
Private domain damage (P) implies more legal liability (R) than public domain damage (Q) [as we know by extrapolation from the case of tooth & foot]. |
|
For horn, public domain damage (Q) implies legal liability (R) enough to make the payment half (S). |
|
Therefore, for horn, private domain damage (P) implies legal liability (R) enough to make the payment half (S). |
This appears to be how R. Tarfon interprets the Sage’s remark, because he then proposes an alternative argument, which manifestly does not rely on an additional premise about proportionality, i.e. is like the Sages’ counter-argument purely a fortiori, and yet succeeds in reaching the same conclusion of full compensation, viz.:
|
Horn damage (P) implies more legal liability (R) than tooth & foot damage (Q) [as we know by extrapolation from the case of public domain]. |
|
For private domain, tooth & foot damage (Q) implies legal liability (R) enough to make the payment full (S). |
|
Therefore, for private domain, horn damage (P) implies legal liability (R) enough to make the payment full (S). |
Even so, the Sages retort dayo again, meaning that they do not accept R. Tarfon’s conclusion of full compensation and still advocate only half compensation. This suggests that their first retort was not essentially a preference for purely a fortiori argument as against a crescendo argument, but only incidentally so. But if so, why did they state their dayo objection in precisely the same terms both times?
Observe here the great logical skill of R. Tarfon. His initial proposal, as we have seen, was an a crescendo argument that the Sages (for reasons to be determined) limited to purely a fortiori. This time, R. Tarfon takes no chances, as it were, and after judicious reshuffling of the given premises offers an argument which yields the same stringent conclusion whether it is read as a crescendo or as purely a fortiori. A brilliant move! It looks like he has now won the debate; but, surprisingly, the Sages again reject his conclusion and insist on a lighter sentence.
How can this be? For a start, how can R. Tarfon using the exact same data construct two structurally different arguments that yield the same conclusion? And moreover, how can the Sages respond to such structurally different arguments in one and the same language? Both times (reportedly) they say: “it is quite sufficient that the law in respect of the thing inferred should be equivalent to that from which it is derived: just as for damage done on public ground the compensation [in the case of horn] is half, so also for damage done on the plaintiff's premises the compensation should not be more than half.”
The answer to these questions becomes evident once we notice how the major premises of R. Tarfon’s two arguments are developed. The major premises are based on generalizations. That “Private domain damage universally implies more legal liability than public domain damage” is known by extrapolation from the specific case of tooth & foot. Similarly, that “Horn damage universally implies more legal liability than tooth & foot damage” is known by extrapolation from the specific case of public domain. The generalities are not textually given or deduced – they are induced. The reason why the two arguments are different is that they are based on two different directions of generalization from the same pool of data.
As regards the Sages’ two dayo statements, the first one cannot concern the generalization leading to the major premise, since the major premise is not based on information about horn damage, but only on information about tooth & foot damage. The Sages’ first remark can only concern R. Tarfon’s assumption that “The payment due is ‘proportional’ to the degree of legal liability,” because it is precisely this tacit premise which makes the stringent conclusion possible. On the other hand, the Sages’ second remark cannot possibly concern an assumption of proportionality in R. Tarfon’s second argument, since he makes no such assumption in it, but argues purely a fortiori. Therefore, the Sages’ second remark must concern the generalization which gives rise to the major premise of R. Tarfon’s second argument.
Thus, whereas the Sages’ first dayo is clearly aimed at inhibiting adoption of the additional premise about proportionality in R. Tarfon’s first argument (which is a crescendo), their second dayo can only be aimed at inhibiting the mental formation of the major premise of R. Tarfon’s second argument (which is purely a fortiori). Thus, although the language used by the Sages is identical in both cases, the technical impacts of their two statements are very different.
What is the Sages’ thinking when they say dayo? It is clear that the Sages realize that the premise about proportionality in R. Tarfon’s first argument is not logically necessary, i.e. it is expendable. It might at first sight seem obvious that compensation for damages should be ‘proportional’ to the degree of responsibility of the accused; but the Sages effectively say: no, this is just an ethical imperative, which may for higher ethical reasons be circumvented at times. What is at stake here is the principle of ‘measure for measure’ (midah keneged midah).
Intuitively, it seems just and fair that the punishment meted out should be proportional to the crime committed. But the Sages’ dayo implies that this principle of justice and equity, although good, cannot always be put into practice. Specifically, when we try to infer a penalty for a crime from the Torah, we cannot apply proportionality; maybe just because determining the exact amount of proportionality is not an exact science, or perhaps because the transition is man-made and therefore fallible.
Rather than risk sentencing someone to possibly excessive punishment, which would constitute a great personal sin for any judge, the Sages wisely stick to the lesser amount specified in the Torah for a lesser crime. It is this higher ethical consideration – the preemption of excessive punishment – which allows the Sages to block application of the ‘measure for measure’ rule, while not denying its truth in principle. The dayo principle, then, is essentially that the penalty given in the Torah for a lesser crime should not be increased for a greater crime not mentioned in the Torah.
Once this principle (the dayo) is understood, based on the Sages’ reaction to R. Tarfon’s first argument, it can equally well – indeed, all the more – be applied to R. Tarfon’s second argument. For, whereas in the first case, the dayo principle was able to neutralize the ‘measure for measure’ principle, a high ethical principle we are strongly attached to, in the second case, which does not appeal to the ‘measure for measure’ principle, the dayo principle is used to block a mere generalization – an inductive act, which may well for a large variety of reasons be interdicted.
This then, briefly exposed, is the thrust of our Mishna, Baba Qama 2:5, which is surprisingly (it should be stressed) the only place in the whole Mishna document where the dayo principle is actually used (let alone discussed). Note well: out of 46 Mishnaic a fortiori arguments, only the above mentioned two by R. Tarfon are subjected to the dayo limitation. It is only in the later Gemara debates that the dayo principle begins to be widely applied (exactly how often, needs still to be determined).
It should be pointed out here, too, that the dayo principle is not mentioned in the lists of hermeneutic principles (midot) attributed to Hillel and R. Ishmael. They mention the qal vachomer argument as the first rule of rabbinic interpretation, but do not mention the usually associated dayo principle. This is also surprising. In truth (or at least in my opinion), the dayo principle could ultimately be applied to any similar form of quantitative reasoning. There is no reason to limit its application to a fortiori argument, as traditionally suggested, even if it emerged historically in that specific context.
Indeed, the two arguments of R. Tarfon could equally well have been read as quantitative analogies, and the dayo principle would still have emerged from the Sage’s two objections to prevent proportional penalties. But if so, if indeed the dayo principle is not intrinsically exclusively connected to a fortiori argument, it should have appeared as an independent rule in the said rabbinical lists. It is surely an important principle, which is also found in the jurisprudence of other nations. So, there are some unanswered questions.
6.Gemara Baba Qama 25a-b
Now, one would have expected all that has been said above concerning Mishna Baba Qama 2:5, our analysis of the qal vachomer arguments involved and of the dayo principle, to have been said in a Gemara commentary on this passage. But, no; surprisingly, nothing of the sort appears in it. Instead, we find the Babylonian Talmud embarking on a set of relatively irrelevant investigations and making some very doubtful claims. We cannot here deal with them all in detail, but the following analysis provides a sample. The Gemara opens with this comment[17]:
“Does R. Tarfon really ignore the principle of dayo? Is not dayo of Biblical origin? As taught: How does the rule of qal vachomer work? And the Lord said unto Moses: ‘If her father had but spit in her face, should she not be ashamed seven days?’ How much the more so then in the case of divine [reproof] should she be ashamed fourteen days? Yet the number of days remains seven, for it is sufficient if the law in respect of the thing inferred be equivalent to that from which it is derived!”
In this passage, the Gemara author (who is anonymous) suggests that, even though the Mishna makes it seem as if R. Tarfon did not know the dayo principle formulated by the Sages, in fact R. Tarfon couldn’t have been unaware of the principle because it is of Torah origin. To prove the latter claim, the Gemara adduces a baraita (a Tannaic statement not part of the Mishna) according to which the argument in Numbers 12:14-15 is a qal vachomer one, whose natural conclusion is fourteen days of shaming, which number is cut back to seven days by application of the dayo principle.
Notice in passing how the baraita’s question “How does the rule of qal vachomer work?” is put in general terms, implying that the answer to it is that qal vachomer argument is intrinsically proportional (i.e. a crescendo). This is, of course, absurd – as purely a fortiori argument is very common in the Tanakh and in the Mishna, and even in the Gemara! In the Tanakh, only 6 out of 46 (13%) of the a fortiori arguments are a crescendo; in the Mishna, only 10 of 46 (22%) are so.
The reason why this passage was specifically focused on by the Gemara should be obvious. This is the only a fortiori argument in the whole Tanakh that is both spoken by God and has to do with inferring a penalty for a specific crime. None of the other four a fortiori arguments in the Torah are spoken by God. And of the nine other a fortiori arguments in the Tanakh spoken by God, two (Jer. 25:29 and 49:12) do concern punishment for sins but not specifically enough to guide legal judgment. Clearly, the Mishna BQ 2:5 could only be grounded in the Torah through Numbers 12:14-15.
Now, this Torah passage reads[18]:
“14. If her father had but spit in her face, should she not hide in shame seven days? Let her be shut up without the camp seven days, and after that she shall be brought in again. 15. And Miriam was shut up without the camp seven days; and the people journeyed not till she was brought in again.”
However, to my mind, the simple reading (pshat) of this Biblical passage, or more specifically of v. 14, is the following pure (i.e. non-proportional) a fortiori argument. Note in passing that it is positive subjectal, going from minor to major.
|
Causing Divine disapproval (P) is a greater offense (R) than causing paternal disapproval (Q). |
|
Causing paternal disapproval (Q) is offensive (R) enough to merit isolation for seven days (S). |
|
Therefore, causing Divine disapproval (P) is offensive (R) enough to merit isolation for seven days (S). |
We could, to be sure, alternatively construe the argument as a crescendo (i.e. as proportional a fortiori), even though there is no mention or hint in the source text of any quantity other than seven days. To do that, we need to add a premise about proportionality – which is easy enough to do, given the intuitive ethical principle of ‘measure for measure’. The argument would then be:
|
Causing Divine disapproval (P) is a greater offense (R) than causing paternal disapproval (Q). |
|
Causing paternal disapproval (Q) is offensive (R) enough to merit isolation for seven days (Sq). |
|
The penalty (S) varies in proportion to the offense (R). |
|
Therefore, causing Divine disapproval (P) is offensive (R) enough to merit isolation for fourteen days (Sp). |
We can in this way claim, as the Gemara does, that the penalty in the case of Divine disapproval was limited to only seven days with reference to the dayo principle. This scenario is conceivable, but far from obvious, since as already shown the source text can be simply read as purely a fortiori argument. The insertion of the additional premise about proportionality is, however, reasonable – we would naturally expect a greater penalty for offending God than for offending one’s father. So, the Gemara’s thesis that the dayo principle must have been tacitly applied by God, since the final conclusion given in the Torah is only seven days, has some credibility.
However, it should be noted that the dayo principle used here is not exactly identical to that used in the Mishna under discussion. In the Mishna, the dayo principle serves to limit the penalty for a greater crime which is not mentioned in the Torah to the specific penalty for the lesser crime which is mentioned in the Torah. In the Mishna, then, the source of information is a Torah law, whereas the conclusion is about something not directly addressed by the Torah. And, as we saw, the motive behind this restriction seems to be the limit or fallibility of human judgment.
On the other hand, in the Num. 12:14 passage, the source of information is the idea that offending one’s father merits seven days isolation – which is not a Torah law, but rather apparently a mere intuition, if not an actual custom – and the conclusion is a Divine fiat. No human judgment is called upon here. So, the analogy between the Num. 12:14 example and the Mishna example is not perfect; it is surely a bit forced. It cannot strictly be said that God was applying the Mishnaic dayo principle when he showed Miriam leniency in limiting her punishment to seven days.
Another important disanalogy to note is that, as we have seen, the Mishnaic dayo principle has (at least) two formal expressions. In relation to the first argument of R. Tarfon, conceived as a crescendo, the Sages’ dayo served to block the additional premise about proportionality; whereas in relation to the second argument of R. Tarfon, conceived as purely a fortiori, the Sages’ dayo served to block the initial generalization leading to the major premise. Clearly, while the presumed dayo application in Num. 12:14 might be compared to the Sages’ first dayo, it bears no resemblance to the Sages’ second dayo!
Indeed, search as we might in the Gemara (BQ 25a-b) commentary relative to our Mishna (BQ 2:5), we will find no evidence that its author is at all aware of the existence of two quite distinct arguments by R. Tarfon in the Mishna, which imply two quite distinct dayo retorts by the Sages. It seems that the Gemara’s author, like many distracted commentators after him, only focused on the first argument, and paid no attention to the second. Thus, while the Gemara may have demonstrated that the Sages’ first dayo was “of Biblical origin,” it did not demonstrate that the Sages’ second dayo was so. Even if the second dayo may ex post facto be argued to be somewhat implicit in the first, this is not actually pointed out in the Gemara.
As far as I could tell, it is only much later in Jewish history that rabbinical commentators realized that the dayo principle has two expressions. In rabbinical parlance, the first dayo by the Sages applies “at the end of the law” (al sof hadin), whereas the second dayo by them applies “at the beginning of the law” (al techelet hadin)[19]. I have not managed to find out who and when, and in what precise context, this distinction and terminology were first introduced. This is an important historical question that requires further research.
I have not to date found any evidence that the distinction between the two types of dayo was consciously and explicitly made in literature of Talmudic times. My guess is that this discovery came centuries later, probably thanks to a Tosafist commentator (though it might have been earlier or later). However, not knowing in what precise commentary, and therefore in what discursive context, the differentiation actually occurred, I cannot tell whether it referred to specifically to the Mishna Baba Qama 2:5 or perhaps arose with some other specific example in mind.
Judging by the vagueness of the terminology that is used by rabbinical commentators today (“at the end,” “at the beginning”), it seems unlikely that the original or subsequent commentators, even if they grasped the application of the distinction in BQ 2:5, fully understood its exact nature (i.e. that the first dayo blocked assumption of proportionality, whereas the second dayo blocked an initial generalization). I believe such exact understanding can only proceed from my above detailed analysis, which is original.
I have here focused on only one or two of the issues that the Gemara (BQ 25a-b) commentary raises. Many more serious criticisms of it can be made. Unfortunately, I do not have the space here to bring them to bear. The interested reader will find them in my book, A Fortiori Logic. Suffices for us to note here, in conclusion, how big a role a fortiori logic plays in Jewish hermeneutics and jurisprudence, and how important it is to have a clear idea of the theoretical aspects of a fortiori argument if we are to fully understand – and independently assess – rabbinical legal discussions.
7.Some rabbinical hermeneutic principles
It is interesting to relate some of the above discussion to some of the rabbinical hermeneutic principles (midot), notably those listed by Hillel the Elder, R. Ishmael ben Elisha and R. Eliezer ben Jose ha-Gelili, which date from Mishnaic times. These principles are intended to facilitate or guide interpretation of Biblical texts, especially with a view to formulating religious, political and civil laws.
The first rule of R. Ishmael[20], the principle of kal vachomer, clearly refers to a fortiori argument. As we have mentioned, apart from the descriptive name, there is very little formal analysis of this form of reasoning in Mishnaic or Talmudic literature, although some attempts at more detailed analysis do appear in later rabbinic discourse. The dayo (sufficiency) principle is usually considered as a tacit component of the kal vachomer principle; but, as we have seen, this need not be the case in practice.
The second rule of R. Ishmael, the principle of gezerah shavah, which is based on the terms having some Biblical wording or intent in common, may be said to constitute simple analogy. This is because (evident) same wording, or (assumed) same ‘intent’ of different wordings, do not provide a sufficiently explicit predicate (R) in common to the subjects compared (P and Q). Words are explicit, but they are incidental to what they verbalize; therefore, the assumption that the Torah intends them as significant enough to justify an inference is open to debate[21]. The same can be said of the twelfth rule of R. Ishmael, which refers to contextual inferences (meinyano, misofo, and the like): such reasoning is simple analogy.
However, the third rule of R. Ishmael, the principle of binyan av, falls squarely under the heading of complex analogy. In fact, our above description of complex analogy is an exact description of binyan av reasoning. When the rabbis want to extend the scope of a Torah law (S), they show that some new subject (P) has some feature (R) in common with the Torah-given subject (Q), and assuming that this feature is the reason for the law (this assumption constitutes a generalization, even if it superficially may seem to be a direct insight), they carry the law over from the given case to the unspecified case.
[1] This essay was first put together in 2014, mostly by verbatim excerpts from my book A Fortiori Logic published a few months earlier. It was slightly edited and expanded in 2019, notably by including the lines relating to qualitative analogy (which I had left out before to save space), and adding some new comments relating to the dayo principle and the section on rabbinic hermeneutic principles.
[2] Notice that the symbols R and S, respectively, happen to match the words “Range” (the middle item always refers to a range) and Subsidiary. P is always the major term, wherever placed, and Q is always the minor term.
[3] The Hebrew distinction of orientation may be historically later than Talmudic – I have not found out exactly when and by whom it was introduced in Judaism.
[4] Note that in these statistics I lump implicational arguments with copulative ones, for simplicity’s sake. See appendices 1, 2 and 4 in A Fortiori Logic for more details on these findings. Regarding the two Talmuds, see appendix 3; and regarding other world literature, ancient and more recent, see appendix 5.
[5] This implication is intended in the sense that a larger number implies every smaller number. For example, if I have $5, then I obviously have $3; 5 includes 3, and 3 does not exclude 5.
[6] More briefly put: ‘If and only if something is Rs or more, then it is S’, which can be expressed still more briefly as: ‘Iff ≥ Rs, then S’.
[7] Again, this implication is intended in the sense that a larger number implies every smaller number.
[8] More briefly put: ‘Iff ≥ Rp, then P’.
[9] To give an example of this important issue: suppose membership in an exclusive club depends on one’s age, level of income and maybe other criteria. In that event, one might well say, “this man is old enough but not rich enough to be admitted” – and here, obviously, the man being old ‘enough’ does not imply he will be admitted, although he may be put on a waiting list until he gets rich ‘enough’ too. Thus, in common discourse, the word ‘enough’ may not signify full sufficiency but merely a tendency towards it. But in the present treatise, we intend the word ‘enough’ in its strict sense.
[10] In The Philosophy of the Talmud, chapter 14 and appendix A. See my analysis of the relevant passages in A Fortiori Logic 22.
[11] Note the stipulation “for things that are both R and S.” I have put this precondition in brackets, because it is in fact redundant, since the minor premise of the a fortiori argument implies anyway that not all things that are R are S, but only those things that have a certain threshold value of R or more of it are S. We should not think of S varying with R as a general proposition applicable to all R (implying that all R are S), but remain aware that this concomitant variation occurs specifically in the range of R where the threshold for S has indeed been attained or surpassed (i.e. where the “R enough to be S” condition is indeed satisfied).
[12] Note the stipulation “for things that are both R and P or Q.” I have put this precondition in brackets, because it is in fact redundant, since the major premise of the a fortiori argument implies anyway that not all things that are R are P and not all things that are R are Q, but only those things that have certain threshold values of R or more of it are P or Q. We should not think of R varying with S as a general proposition applicable to all S (implying that all S are R), but remain aware that this concomitant variation occurs (at least) specifically in the range of R where the thresholds for P and Q have indeed been attained or surpassed (i.e. where the “R enough to be P” and “R enough to be Q” conditions are indeed satisfied).
[13] See his Rhetoric 2:23 and Topics 2:10, 3:6. See my analysis of these relevant passages in A Fortiori Logic 6.1.
[14] See his Topics, §23. 68-71. See my analysis of these relevant passages in A Fortiori Logic 6.5.
[15] See chapter 14 of that work. See my analysis of the relevant passages in A Fortiori Logic 9.10.
[16] The extracts from the Talmud quoted here were found on the Internet at: www.halakhah.com/pdf/nezikin/Baba_Kama.pdf. I have made minor modifications to the text, such as changing the spelling of Kal wa-homer and Dayyo. All explanations in square brackets in the Gemara are as in the original.
[17] Source already cited.
[18] From Soncino Chumash.
[19] See Encyclopedia Talmudit, article on the dayo principle.
[20] Given at the beginning of the Sifra (a halakhic midrash).
[21] In other words, the traditional Judaic belief (or dogma) that names are part of the nature of the things they name, if not their very essence, is – as far as formal logic is concerned – only a theory. There is nothing obvious or axiomatic about it. It is a hypothesis that must remain open to scrutiny and testing like any other. Modern linguistics would deny this hypothesis in view of the demonstrable fact that all languages, including Hebrew, have evolved over time.